Задача: найти основания трапеции

Рассмотрим задачу, в которой необходимо найти основания трапеции (по материалам ОГЭ по математике, №26 в спецификации 2018 года).

Задача. Углы при одном из оснований трапеции равны $77^0$ и $13^0$ , а отрезки соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции

Источник. Решу ОГЭ. Образовательный портал для подготовки к экзаменам. https://math-oge.sdamgia.ru/test?theme=85, №9.

Подсказка №1

Достроить боковые стороны трапеции AB и CD до пересечения, получится треугольник ASD. Он прямоугольный, т.к. сумма углов при основании трапеции $77^0+13^0=90^0$

Подсказка №2

Надо доказать, что медиана SN треугольника ASD пересекает отрезок BC в его середине — точке M.
Медиана, проведенная к гипотенузе прямоугольного треугольника равна половине гипотенузы

Подсказка №3

Докажем, что медиана SN треугольника ASD пересекает отрезок BC в его середине — точке M.
Треугольники BSC и ASD — подобны, т.к. BC параллельно AD. Из подобия треугольников следует:

$\frac{SB}{SA}=\frac{BC}{AD}$

Треугольники BSM и ASN — подобны, т.к. BC параллельно AD. Из подобия треугольников следует:

$\frac{SB}{SA}=\frac{BM}{AN}=\frac{BM}{\frac{1}{2}AD}$

Получаем:

$\frac{BC}{AD}=\frac{BM}{\frac{1}{2}AD}$

$BC=2BM$

Подсказка №4

Обозначим $BC=a$ , $AD=b$ , $KL=m$ , $MN=n$ .
$KL$ — средняя линия трапеции, поэтому $m=\frac{a+b}{2}$ или $a+b=2m$
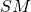
$SM$ — медиана в прямоугольном треугольнике BSC, поэтому $SM=\frac{a}{2}$
$SN$ — медиана в прямоугольном треугольнике ASD, поэтому $SN=\frac{b}{2}$
Получаем соотношение $\frac{a}{2}+n=\frac{b}{2}$ или $a+2n=b$
Остается решить систему уравнений:

$\left\{\begin{aligned}a+b=2m,\\a+2n=b.\\ \end{aligned}\right.$

Ответ

Ответ: $BC=1, AD=21$

Задача: найти основания трапеции

Добавить комментарий Отменить ответ