Приведем решение стереометрической задачи из материалов ЕГЭ (задание с развернутым ответом)
Задача. Образующая конуса равна диаметру его основания. В основание конуса вписан правильный треугольник. Через середину высоты конуса и сторону треугольника проведена плоскость ![]() .
.
а) Докажите, что угол между плоскостью основания конуса и плоскостью ![]() равен
равен ![]() .
.
б) Найдите площадь сечения плоскостью a шара, вписанного в конус, если радиус основания конуса равен ![]() .
.
Источник: ЕГЭ 2017. Математика. Профильный уровень. 30 вариантов типовых тестовых заданий и 800 заданий части 2 / И.В.Ященко, М.А.Волчкевич, И.Р.Высоцкий. – М.: Экзамен, 2017. – 215 с.
Дано:
конус с вершиной ![]()
![]() , где
, где ![]() — диаметр основания конуса
— диаметр основания конуса
![]() — правильный треугольник, вписанный в основание конуса
— правильный треугольник, вписанный в основание конуса
![]() — высота конуса
— высота конуса
![]() — середина
— середина ![]()
плоскость сечения ![]() проходит через
проходит через ![]() и отрезок
и отрезок ![]()
![]()
в конус вписан шар
Доказательство (пункт а)
Для доказательства того, что угол между плоскостью основания конуса и плоскостью ![]() равен
равен ![]() , сделаем дополнительные построения. Построим
, сделаем дополнительные построения. Построим ![]() — середину
— середину ![]() , построим
, построим ![]() ,
, ![]() ,
, ![]() ,
, ![]() (рис. 1).
(рис. 1).
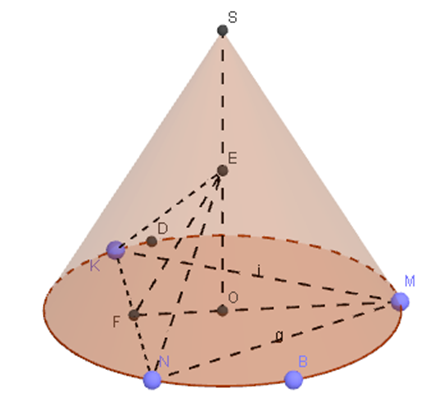 |
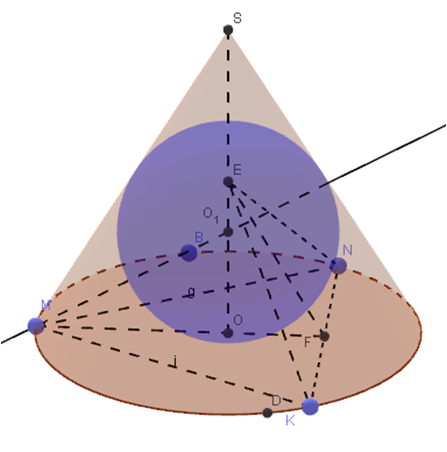 |
| Рис. 1. | Рис. 2. |
Поскольку образующая конуса равна диаметру, то ![]() . Треугольник
. Треугольник ![]() — прямоугольный и катет равен половине гипотенузы, значит угол
— прямоугольный и катет равен половине гипотенузы, значит угол ![]() .
.
![]()
![]()
Рассмотрим ![]() :
: ![]() — медиана,
— медиана, ![]() — центр описанной окружности, значит
— центр описанной окружности, значит ![]() или
или ![]() . Т.к.
. Т.к. ![]() , то
, то ![]() .
.
Найдем ![]() . В
. В ![]() :
:
![]()
![]()
Из теоремы о трех перпендикулярах следует, что ![]() , поэтому угол между плоскостью сечения
, поэтому угол между плоскостью сечения ![]() и плоскостью основания конуса равен
и плоскостью основания конуса равен
![]()
Скачать интерактивную 3D-модель
Примечание. Описание построения интерактивной модели к задаче можно посмотреть здесь.
Решение (пункт б):
Построение
Необходимо вписать шар в конус. Рассмотрим произвольное осевое сечение конуса. Поскольку образующая конуса равна диаметру основания, то в осевом сечении находится равносторонний треугольник. Центр вписанного в конус шара совпадает с центром окружности, вписанной в треугольник осевого сечения. Центр вписанной окружности лежит на пересечении биссектрис, высота конуса ![]() — биссектриса треугольника осевого сечения. Осталось построить еще одну биссектрису, получаем центр вписанного в конус шара. Строим биссектрису
— биссектриса треугольника осевого сечения. Осталось построить еще одну биссектрису, получаем центр вписанного в конус шара. Строим биссектрису ![]() , строим точку
, строим точку ![]() — точку пересечения биссектрисы
— точку пересечения биссектрисы ![]() и высоты
и высоты ![]() . Строим сферу с центром в точке
. Строим сферу с центром в точке ![]() и радиусом
и радиусом ![]() . Получили требуемый чертеж к задаче (рис. 2).
. Получили требуемый чертеж к задаче (рис. 2).
Анализ чертежа показывает, что дальнейшие рассуждения нужно проводить на осевом сечении, проходящем через точку ![]() – середину стороны
– середину стороны ![]() правильного треугольника, вписанного в основание конуса (рис. 3,4).
правильного треугольника, вписанного в основание конуса (рис. 3,4).
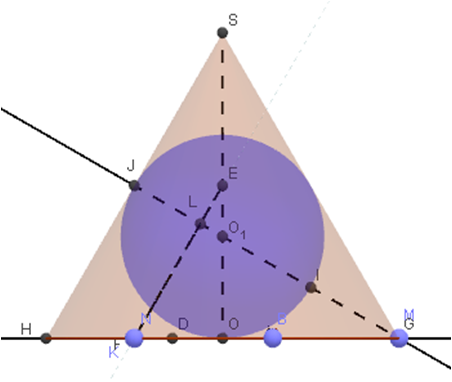 |
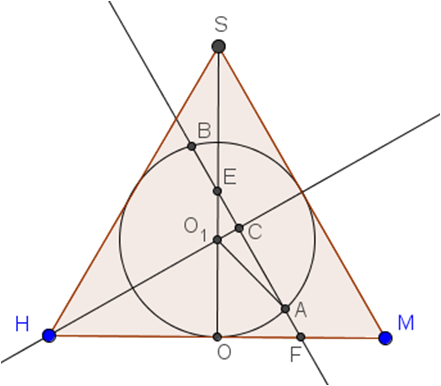 |
| Рис. 3. Осевое сечение, проходящее через точку |
Рис. 4. Осевое сечение |
Ответим на вопрос задачи – найдем площадь сечения шара. Ясно, что это – круг, поэтому его площадь полностью определяется радиусом.
Скачать интерактивную 2D-модель (плоскость осевого сечения).
Примечание. Описание построения интерактивной модели к задаче можно посмотреть здесь.
Решение
1) Если радиус основания конуса равен ![]() , то сторона треугольника
, то сторона треугольника ![]() равна
равна ![]() .
.
2) Радиус вписанной окружности
![]()
3)
![]()
4) ![]() ;
;
5) катет, лежащий напротив угла в ![]() равен половине гипотенузы, значит в треугольнике
равен половине гипотенузы, значит в треугольнике ![]() :
:
![]()
6) в треугольнике ![]() по теореме Пифагора:
по теореме Пифагора:
![]()
7) Искомая площадь сечения
![]()